Data Structures and Algorithms (CS506)

Lab Assignment 4

Selection problem: The input is a list of n integers, and an integer k. The selection problem is to find the kth largest element. Below, we describe two algorithms to solve this problem. Your job is to implement both the algorithms.

a. Algorithm 1a: The algorithm reads n integers into an array. Apply BUILD-MAX-HEAP algorithm to this array. Then apply k times EXTRACT-MAX operations. Return the last element extracted from the heap as the answer. Clearly, the running time of this algorithm is O(n + k log n).

Sol1a. Download the Solution1a file. Open terminal and execute it by running ./solution1a.o command. Give inputs to get ourputs.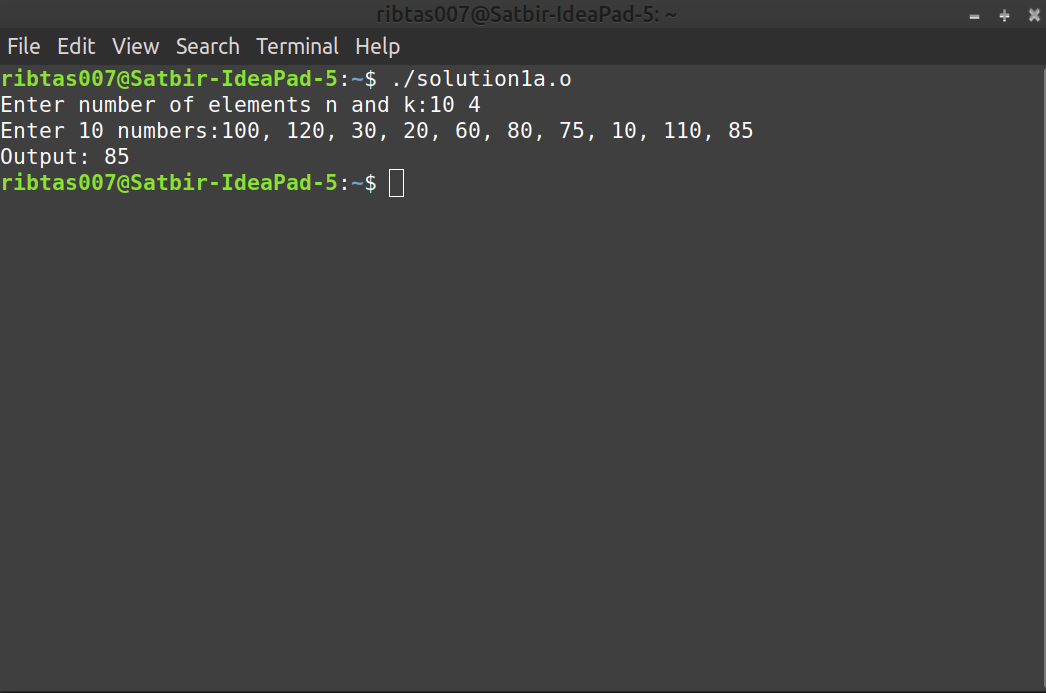

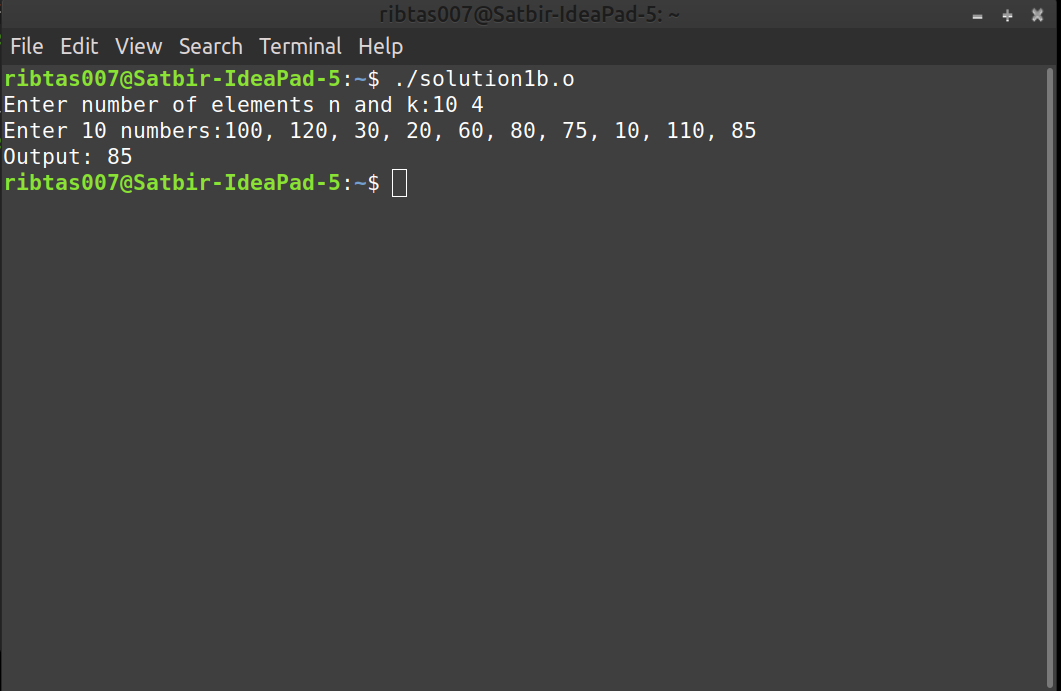
b. Algorithm 1b: At any point of time the algorithm maintain a set S of the k largest elements. After the first k elements are read, when a new element is read it is compared with the kth largest element, which we denote by S_k . Note that S_k is the smallest element in S. If the new element is larger, then it replaces S_k in S. S will then have a new smallest element, which may or may not be the newly added element. At the end of the input, the algorithm find the smallest element in S and return it as the answer.

You are instructed to use min-heap to implement S. The first k elements are placed into the min-heap in O(k) time. For the remaining elements do the following: test in O(1) time whether the new element goes into S (min-heap), if yes, delete S_k (the root element of the min-heap S) and insert the new element. Clearly, inserting the new element takes O(log k) time. Thus total time required: O(k + (n − k) log k) = O(n log k).

Note: We can solve this problem in O(n) average time. This is just for your information.

Test Case:
```
         Input: Enter number of elements n and k: 10 4
         Enter 10 numbers: 100, 120, 20, 30, 10, 110, 90, 65, 40, 50
         Output: 90
```
Sol1b. Download the Solution1b file. Open terminal and execute it by running ./solution1b.o command. Give inputs to get ourputs.